ECE_Legends: Verilog Datatypes & Operators: Unit 2

LOGIC VALUES:

· 1 signifies the 1 or high or true level

· 0 signifies the 0 or low or false level.

Two additional levels are also possible – designated as x and z.
Here x represents an unknown or an uninitialized value. This corresponds to the don’t-care case in logic circuits.
z represents/signifies a high impedance state. This is possible when a signal line is tri-stated or left floating.

DATA TYPES:

A value in a digital system can basically be represented either as net or variable in Verilog. The data handled in Verilog fall into two categories

o Net data type

o Variable data type

Data type of each variable or signal has to be declared prior to its use.

1. NET :

· The net data type is specific for connecting two elements.

· The most important net data type is wire.

· As the name implies, this data type acts simply as a wire connecting two elements.

· Such a net carries the value of the signal it is connected to and transmits to the circuit blocks connected to it.

· If the driving end of a net is left floating, the net goes to the high impedance state.

· A net can be specified in different ways.

o wire: It represents a simple wire doing an interconnection. Only one output is connected to a wire and is driven by that.

o tri: It represents a simple signal line as a wire. Unlike the wire, a tri can be driven by more than one signal outputs.

2. VARIABLE :

· A variable is an abstraction for a storage device.

· The variable data type can be used to represent generated data till it changes.

· It can be declared through the keyword reg and stores the value of a logic level: 0, 1, x, or z.

· A net or wire connected to a reg takes on the value stored in the reg and can be used as input to other circuit elements.

· But the output of a circuit cannot be connected to a reg. The value stored in a reg is changed through a fresh assignment in the program.

· Useful variable data types are time, integer, real, and realtime.

A net or variable data type can get one of four predefined values. These are

§ 0 corresponds to logic level zero.

§ 1 corresponds to a logic level one.

§ x represents the undefined logic level.

§ z represents high impedance.

Constants

Verilog provides constants in addition to variables and nets. Verilog provides three different ways to define constant values, one of which is using `define as in

`define constant_name constant_value

The `define compiler directive replaces 'constant_name with constant_value.

For example:

`define wordsize 16

reg [1: wordsize] data;

causes the string wordsize to be replaced by 16. It then shows how data is declared to be a reg of width wordsize.

Another method to create constants is to use the parameter keyword as follows:

parameter constant_name = constant_value;

For example,

parameter msb = 15; // defines msb as a constant value 15

parameter [31:0] decim = 1'b1; // value converted to 32 bits

Another method to make constants is using localparam.

localparam constant_name = constant_value;

The localparam is similar to the parameter, but it cannot be directly changed. The localparam can be used to define constants that should not be changed.

Arrays (or) Vector

Arrays in Verilog can be used while modelling the repetition. Digital systems often use memory arrays. Verilog arrays can be used to create memory arrays and specify the values to be stored in these arrays. In order to use an array in Verilog, we must declare the array upper and lower bound. There are two positions to declare the array bounds:

In one option, the array bounds are declared between the variable type (reg or net) and the variable name, and the array bound means the number of bits for the declared variable. If the array bound is defined as [7:0] as shown in the following example,

reg [7:0] eight_bit_register;

the register variable eight_bit_register can store one byte (eight bits) of information. The 8-bit register can be initialized to hold the value 00000001 using the following statement:

eight_bit_register 5 8'b00000001;

As a second option, array bounds can be declared after the name of the array. In the declaration that follows, rega is an array of n 1-bit registers while regb is a single n-bit register.

reg rega [1:n]; // This is an array of n 1-bit registers

reg [1:n] regb; // This is an n-bit register

We can define multiple 8-bit registers in one array declaration. In this case, additional upper and lower bound(s) must be declared after the name of the array. In the example that follows, 16 registers are declared; each register can store one-byte (8-bit) vector information.

reg [7:0] eight_bit_register_array [15:0];

The foregoing declaration means that each of the 16 variables in the array can have 8-bit vector information. This array can be initialized as follows:

eight_bit_register_array[15] = 8'b00001100;

eight_bit_register_array[14] = 8'b00000000;

. . . . . . . .

eight_bit_register_array[1] = 8'b11001100;

eight_bit_register_array[0] = 8'b00010001;

Arrays can be created of various data types. Arrays of wires and integers can be declared as follows:

wire wire_array [5:0]; // declares an array of 6 wires

integer inta [1:64]; // declares an array of 64 integer values

Matrices

Multidimensional array types may also be defined with two or more dimensions. The following example defines a 2-dimensional array variable in an initial statement, which is a matrix of integers with four rows and three columns with 8-bit elements:

reg [7:0] matrixA [0:3][0:2] = { { 1, 2, 3},

{ 4, 5, 6},

{ 7, 8, 9},

{10, 11, 12} };

The array element matrixA[3][1] references the element in the fourth row and second column, which has a value of 11.

EX: BASIC VECTOR OPERATION IN VERILOG

TestBench file for Basic Vectoroperation in Verilog

Result:

Operators in Verilog

An operator, in many ways, is similar to a simple mathematical operator. They receive one or two inputs and generate a single output. Operators enable synthesis tools to choose the desired hardware elements.

We can categorize operators based on:

Number of Operands
Operation

Operators in Verilog based on the number of Operands

Depending on how many operands are used in an expression, operators are classified as:

Unary
Binary
Ternary

Unary operators

Unary operators need only one operand. For example, arithmetic operators for representing sign (+,-), negation operator (!,~), reduction operator (&, |, ~, ^).

Binary operators

A binary operator requires two operands to perform operations. The majority of the operators available in Verilog requires two operands. Addition, logic operations, multiplication, etc.

Ternary operators

Ternary operators require three operands. For example, conditional operator(? :).

We will look at examples for each of the above in detail as we proceed.

Operators in Verilog based on Operation

We can also classify operators based on what operation they perform on given data.

Arithmetic operators

This operator is gonna take us to good old school days.

5+2 = 7 // addition

6-4 = 2 // subtraction

2*3 = 6 // multiplication

20/5 = 4 // division

Arithmetic operators are used to perform basic math calculations. They perform a specific operation on two numeric values and return a single numeric value.

Arithmetic operators play a significant part in describing hardware units such as Arithmetic logic Unit (ALU). Therefore, Verilog has provided us with the following arithmetic operators.

Expression	Operator used	Operation performed
a + b	+	Add
a – b	–	Subtract
a * b	*	Multiply
a / b	/	Divide
a % b	%	Modulus(the remainder is given as result)
a ** b	**	Power(exponent)

What about signed numbers?

Verilog also has the provision for representing signed numbers. We use ‘+’ and ‘-‘ to represent positive and negative numbers. In short, ‘+’ and ‘-‘ can be used in both unary and binary forms. Unary is for representing signed numbers and binary for calculations.

//unary arithmetics

-4 // negative number

+5 // positive number

//binary arithmetics

5+4 // addition

6-4 // subtraction

Note: It is advisable to write negative numbers in real or integer format. Since Verilog converts negative numbers into 2’s complement internally, writing in <size>'<base><number> format will yield incorrect result.

-10/5 // yield correct result

- 32'd10/5 // will yield an incorrect result

Now that we have an idea of what arithmetic operators are, we can see how they are used in Verilog using a sample program as an example.

module arithmetic_operations;

reg[7:0] data1;

reg[7:0] data2;

initial

begin

data1 = 45;

data2 = 9;

$display ("add(data1,data2) = %d", data1 + data2)

$display ("subtract(data1,data2) = %d", data1 - data2);

$display ("multiply(data1,data2) = %d", data1 * data2);

$display ("divide(data1,data2) = %d", data1 / data2);

$display ("modulus(data1,data2) = %d", data1 % data2);

$display ("power(data2,2) = %d", data2 ** 2);

end

endmodule

Simulation log

add(data1,data2) = 54

subtract(data1,data2) = 36

multiply(data1,data2) = 149

divide(data1,data2) = 5

modulus(data1,data2) = 0

power(data2,2) = 81

Example 1:

Arithmetic Operations on a Constant and Vector in Verilog

Testbench File for Arithmetic Operations on a Constant and Vector in Verilog

Results: Result of arithmetic operations on a constant and vector in Verilog

Working principles of arithmetic operations including a constant, we provide the testbench file above. Here, input vector to be processed is taken as 8’h07. Arithmetic operation results are provided (in hexadecimal form) in above Fig. As can be seen in this figure, only the integer part of the division operation is kept.

example 2:

Arithmetic Operations on Two Eight-bit Vectors in Verilog.

Testbench File for Arithmetic Operations on Two Eight-bit Vectors in Verilog

Result of arithmetic operations on two eight-bit vectors in Verilog.

Logical Operators

Logical operators perform a logical operation on the logical value of the operands and tell you whether it is true or false, i.e., it returns a boolean value. For example:

Let’s say we have to perform logical and operations between 3 (non-zero) and 0 (zero). Hence, Logical value of 3 is true(1) and for 0, it is false(0). Therefore, AND of true and false will give you false (0).

These are the logical operators available in Verilog.

Expression	Operator	Operation	Description
A && B	&&	Logical – and	The result will be 1 (true ) if A and B are true
A \|\| B	\|\|	Logical – or	The result will be true if either A or B is true
!A	!	Logical negation	Will convert to zero if A is non-zero or 1 A is zero or false value

Here’s how Verilog performs logical operations.

module logical_operation;

reg[7:0] A;

reg[7:0] B;

reg[1:0] din1;

reg[1:0] din2;

wire out;

initial

begin

A = 3;

B=0;

din1 = 2’b0x;

din2 = 2’b10

$display(“logical_AND(A,B)=%b”, A &&B);

// Equivalent to logical-1 && logical-0

$display(“logical_OR(A,B)= %b“, A ||B);

// Equivalent to logical-1 || logical-0

$display(“logical_NOT(A) = %b“, !A);

// Equivalent to not(logical-1)

$display(“logical_NOT(B) = %b“, !B);

// Equivalent to not(logical-0)

$display(“logical_AND(din1,din2) = %b“, din1 &&din2);

// Equivalent to ( x && logical-1)

$display(“out = %b“, (A==2)&&(B==3);

// Evaluates 1 if both A=2 and B=3 are true otherwise false.

end

endmodule

Simulation log

logical_AND(A,B) = 0

logical_OR(A,B) = 1

logical_NOT(A) = 0

logical_NOT(B) = 1

logical_AND(din1,din2) = x;

out = 0

Bit-wise Operators

Verilog supports the use of a bit-wise operator. This operator is a bit of an odd cross between a logical operator and an arithmetic operator. They take each bit in one operand and perform the operation with the corresponding bit in the other operand. If one of the operands is shorter than the other, the length will be made the same by adding zeros on the shorter operand. It’s a bit confusing. Check out the example below.

For example: bitwise AND of a = 3(11) and b=2 (00). Bitwise AND is similar to concatenating a[1] & b[1] and a[0] & b[0] which gives a result 00.

We will get a better understanding when we go through the simulated output of this code.

module bitwise_logical_operations;

reg[3:0] X, Y, Z;

initial

begin

X=4’b1010;

Y=4’b1101;

Z=4’b10x1;

$display (“~X = %b“, ~X); // Negation

$display (“X & Y = %b“, X & Y); // Bitwise AND

$display (“X | Y = %b“, X | Y); // Bitwise OR

$display (“X ^ Y = %b“, X ^ Y); // Bitwise XOR

$display (“X ^~ Y = %b“, X ^~ Y); // Bitwise XNOR

$display (“X & Z = %b“, X & Z); // Bitwise AND

end

endmodule

Simulation log

~X = 0101

X & Y = 1000

X | Y = 1111

X ^ Y = 0111

X ^~ Y = 1000

X & Z = 10x0

Reduction Operators

Unlike logical and bitwise logical operators, the Reduction operator is a unary operator. This operand is useful for converting a multi-bit vector into a single bit scalar value. It performs bit by bit logical operation on the vector operand and returns a boolean value.

For example,

&(1011) = 1 & 0 & 1 & 1 = 0 // reduction SWand of 1011

Verilog has provided us with the following types of reduction operators.

Expression	Operator	Description
&A	&	Performs bitwise AND operation on A
\|A	\|	Performs bitwise OR operation on A
^A	^	Performs bitwise XOR operation on A

Note: reduction NAND, reduction NOR and reduction XNOR are performed by inverting results of reduction AND, reduction OR and reduction NOT respectively.

Here’s the code for understanding how reduction operator is described in Verilog

module reduction_operators;

reg[5:0] X;

initial

begin

X = 4'b1010;

$display ("&X = %b", &X);

$display ("|X = %b", |X);

$display ("^X= %b", ^X);

$display("~^X = %b", ~(^X)); //XNOR of X

end

endmodule

Simulation log

&X = 0

|X = 1

^X= 0

~^X = 0

Difference between logical, bitwise logical, and reduction operators?

Logical	Bitwise logical	Reduction
Binary operator (except negation)	Binary operator (except negation)	Unary operator
Returns a 1-bit Boolean value	The return value is of the same size as the operands	Returns a 1-bit Boolean value
Evaluate the logical values of the operands and then perform a logical operation.	Performs a logical operation on each bit of operand with the corresponding bit of other operands	Evaluate each bit of vector operand and convert it into a scalar by performing a logical operation.

In short, even though the functionalities look similar, there is a difference in how the above operators perform on the operands.

Relational operators

If we want to check the relation between the given operands, then we use relational operators. Relational operators test the relation between operands and return a 1 or 0.

Expression	Operator	Description
a>b	< (greater than)	Returns 1 if a is greater than b
a<b	< (less than)	Returns 1 if a is less than b
a<=b	<= (less than or equal to)	Returns 1 if a is either less than or equal to b
a>=b	>= (greater than or equal to)	Returns 1 if a is either greater than or equal to b

An example code will help us to understand how relational operators work in Verilog.

module relational_operation;

reg[7:0] A;

reg[7:0] B;

reg[5:0] X;

reg[5:0] Y;

reg[5:0] Z;

initial

begin

A = 3;

B=4;

X = 4’b1010;

Y = 4’b1101;

Z = 4’b1xxx;

$display(“Is A less than or equal to B = %b”, A<=B);

$display(“Is A greater than B = %b”, A>B);

$display(“Is Y greater than or equal to X = %b”, Y>=X);

$display(“Is A less than or equal to B = %b”, A<=B);

$display(“Is Y less than Z = %b”, Y<Z);

end

endmodule

Simulation log

Is A less than or equal to B = 1

Is A greater than B = 0

Is A less than or equal to X = 1

Is Y less than Z = x

Equality Operator

Like Relational operators, Equality operators are also used for relation checking. These operators test whether the operands are the same or not. They return 1 if both the operands are the same and 0 if they are not.

A list of equality operators in Verilog is given below.

Expression	Operator	Description
A = = B	= =	A equal to B, the result is unknown if a or b has z(high impedance) or x(unknown)
A != B	! =	A not equal to B, the result is unknown if a or b has z(high impedance) or x(unknown)
A = = = B	= = =	A equal to B including x(unknown) and z(high impedance)
A ! = = B	! = =	A not equal to B including x(unknown) and z(high impedance)

As per the table, we can see that there are two types of equality operators:

Logical Equality (==,!==): In this case, if one of the operand bits has an x(unknown) or z(high impedance), the resultant will be x.
Case Equality (===,!===): Here, the x(unknown) and z(high impedance) in operand bits are included during the comparison. So the result will be either true (1) or false (0).

Let’s see how Verilog performs equality operation with the help of the code below:

module equality_operators;

reg[7:0] A;

reg[7:0] B;

reg[5:0] M;

reg[5:0] N;

reg[5:0] X;

reg[5:0] Y;

reg[5:0] Z;

initial

begin

A = 3;

B=4;

X = 4’b1010;

Y = 4’b1101;

Z = 4’b1010;

M = 4’b1xxz;

N = 4’b1xxx;

$display (“Is A equal to B = %b”, A == B);

$display (“Is X not equal to Y = %b”, X != Y);

$display (“Is A equal to B = %b”, A == B)

$display (“Is Z equal to M = %b”, Z === M);

$display (“Is Z equal to N = %b”, Z === N)

$display (“Is M not equal to N = %b”, M !== N);

end

endmodule

Simulation log

Is A equal to B = 0

Is X not equal to Y = 1

Is A equal to B = 0

Is Z equal to M = 0

Is Z equal to N = 0

Is M not equal to N = 1

Shift Operators

Shift operators are used to shift data in a variable. This operator is essential for modelling hardware elements like shift registers, shift and add multipliers, etc.

There are two types of shift operations:

Logical Shift

A Left Logical Shift of one position moves each bit to the left by one. The vacant least significant bit (LSB) is filled with zero and the most significant bit (MSB) is discarded.
A Right Logical Shift of one position moves each bit to the right by one. The least significant bit is discarded and the vacant MSB is filled with zero.

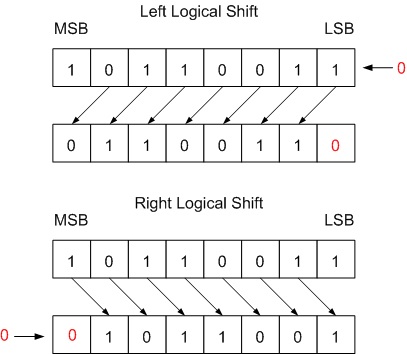
Fig. 1 Logical Shift by one bit

Arithmetic Shift

A Left Arithmetic Shift of one position moves each bit to the left by one. The vacant least significant bit (LSB) is filled with zero and the most significant bit (MSB) is discarded. It is identical to Left Logical Shift.
A Right Arithmetic Shift of one position moves each bit to the right by one. The least significant bit is discarded and the vacant MSB is filled with the value of the previous (now shifted one position to the right) MSB.

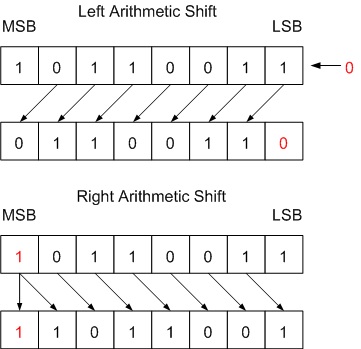
Fig. 1 Left and Right Arithmetic Shift by One Bit

Arithmetic Shift operations can be used for dividing or multiplying an integer variable.

The shift operators provided in Verilog are:

Operator	Description
>>	Right shift
<<	Left Shift
>>>	Arithmetic Right Shift
<<<	Arithmetic Left shift

We will be able to gain a clear understanding of how a shift operator works in Verilog from the below code:

module shift_operators;

reg [3:0] var1 = 4'b1000;

reg signed [3:0] var2 = 4'b1000

initial

begin

//left shift

$display("%b", var1 << 1);

$display("%b", $signed(var1) <<< 1); // Cast as signed

$display("%b", var2 <<< 1); // Declared as signed type

// Right Shift

$display("%b", var1 >> 2);

$display("%b", $signed(var1) >>> 2); // Cast as signed

$display("%b", var2 >>> 2) ; // Declared as signed type

end

endmodule

Simulation log

0000

0010

1110

Concatenation Operators

Concatenation operators are used to join different bits of data into one. Concatenations are expressed using the brace characters { }, with commas separating the expressions within.

We will get a better understanding of the working of the concatenation operator from the simulated output of the code below.

module concatenation_operator;

reg A;

reg[1:0] B, C;

reg[2:0] D;

initial

begin

A = 1'b1;

B= 2'b00;

C = 2'b10;

D = 3'b110;

$display ("concatenation(B,C) = %b", {B,C});

// two 2 bits joined to form 4 bit number

$display ("concatenation(A,B,C,D,3'b001) = %b", {A,B,C,D,3'b001});

$display ("concatenation(A,B[0],C[1]) = %b", {A,B[0],C[1]});

end

endmodule

Simulation log

concatenation(B,C) = 0010

concatenation(A,B,C,D,3'b001) = 10010110001

concatenation(A,B[0],C[1]) = 101

Replication operator

The replication operator is used to replicate a group of bits n times. It takes the format {n{m}}, where n indicates replication multiplier i.e., how many times m should be repeated.

For example, in {3{2’b01}} 3 is the repetition multiplier and 2’b01 is what will be replicated 3 times.

It is important to note that the repetition multiplier must be a constant.

Look at the Verilog code and simulated output below to see how the replication operator works.

module replication_operator;

reg A;

reg[1:0] B, C;

reg[2:0] D;

wire Y;

initial

begin

A = 1'b1;

B= 2'b00;

C = 2'b10;

D = 3'b110;

$display ("replicating A = %b", {4{A}});

$display ("replicating A and B = %b", {{4{A}},{2{B}}});

$display ("replicating A,B,C = %b", {{4{A}},{2{B}},{C}});

end

endmodule

Simulation log

replicating A = 1111

replicating A and B = 11110000

replicating A,B,C = 1111000010

example: Concatenation and Replication Operations in Verilog

Testbench File for Concatenation and Replication Operations in Verilog

Result of concatenation and replication operations in Verilog

Conditional Operator

The conditional operator selects an expression for evaluation depending on the value of the condition.

condition?true_expression:false_expression

If the condition is evaluated as false (or zero value), then false_expression is evaluated and used as a result of an entire expression.

For example

assign out = enable?data1:data2;

The above statement means that out will be assigned data1 if enable is true(1) or zero if enable is false(0).

Verilog makes use of the conditional operator in order to build tri-state buffers and multiplexers.

Let’s see how the conditional operator can be used practically.

module conditional;

reg check = 1'b1;

wire out;

assign out = check ? 1'b1 : 1'b0;

initial

begin

#1;

$display("OUTPUT: %s", check ? "HI THERE" : "POTATO");

$display("Value of out: %b", out);

$display("%h", (10 > 5) ? 16'hABCD : 16'h1234);

$display("%s", (1 == 1) ? "YES, ONE EQUALS ONE" : "HOW DID YOU GET HERE");

end

endmodule

Simulation log

OUTPUT: HI THERE

Value of out: 1

abcd

YES, ONE EQUALS ONE

Operator Precedence in Verilog

We have discussed the different operators that we can use in Verilog. Is it possible to use multiple operators in a single expression? Undoubtedly, yes. Then how do we choose which operation to perform first?

That is when the operator precedence table comes to play.

This table describes the order in which the operators are executed.

Precedence	Operators	Operator Symbols
Highest	Unary Multiply Divide, Modulus	+ – ! ~ * / %
	Add Subtract Shift	+ – << >>
	Relational Equality	< <= > >= == !== === !===
	Reduction Logical	& ~& ^ ^~ \| ~\| && \|\|
Lowest	Conditional	?:

For example:

A && B || C && D

// same as (A && B) || (C&&D) expression in parenthesis evaluated first

But, it is better to use brackets rather than depending entirely on the precedence of operators. This will ensure the readability of the expression and correctness of the result.

Tabular summary

So, we have gone through all the operators that Verilog has provided. Let’s summarize the operators that we have learned.

Operator Type	Operator Symbol	Operation performed	Number of operands
Arithmetic	*	Multiply	Two
	/	Divide	Two
	+	Add	Two
	–	Subtract	Two
	%	Modulus	Two
	**	Power(exponent)	Two
Logical	!	Logical negation	One
	&&	Logical and	Two
	\|\|	Logical or	Two
	^	Logical xor	Two
Relational	>	Greater than	Two
	<	Less than	Two
	>=	Greater than or equal to	Two
	<=	Less than or equal to	Two
Equality	==	Equality	Two
	!=	Inequality	Two
	===	Case equality	Two
	!===	Case inequality	Two
Bit-wise	~	Bit-wise negation	One
	&	Bit-wise and	Two
	\|	Bit-wise or	Two
	^	Bit-wise xor	Two
	^~	Bit-wise xnor	Two
Reduction	&	Reduction and	One
	~&	Reduction nand	One
	\|	Reduction or	One
	~\|	Reduction nor	One
	^	Reduction xor	One
	~^	Reduction xnor	One
Shift	>>	Right shift	Two
	<<	Left shift	Two
	>>>	Arithmetic right shift	Two
	<<<	Arithmetic left shift	Two
Concatenation	{}	concatenation	Any number
Replication	{{}}	Replication	Any number
Conditional	?:	Conditional	Three

Application on Data Types and Operators

Here we will construct a primitive calculator to add, subtract, multiply, and divide two four-bit numbers on the Basys3 board. Input bits and the operation type is represented by switches on the board. Output bit values are represented by LEDs on the board, Verilog description of the calculator.