AVL TREE

 AVL TREE

 

The first type of self-balancing binary search tree to be invented is the AVL tree. The name AVL tree is coined after its inventor's names − Adelson-Velsky and Landis.

In AVL trees, the difference between the heights of left and right subtrees, known as the Balance Factor, must be at most one. Once the difference exceeds one, the tree automatically executes the balancing algorithm until the difference becomes one again.

In an AVL tree, the heights of the two sub-trees of a node may differ by at most one. Due to this  property, the AVL tree is also known as a height-balanced tree.

AVL trees are self-balancing, which means that the tree height is kept to a minimum so that a very fast runtime is guaranteed for searching, inserting and deleting nodes, with time complexity  O(log n).

In its structure, it stores an additional variable called the BalanceFactor. Thus, every node has a balance factor associated with it. 

The balance factor of a node is calculated by subtracting the height of its right sub-tree from the height of its left sub-tree. A binary search tree in which every node has a balance factor of –1, 0, or 1 is said to be height balanced. A node with any other balance factor is considered to be unbalanced and requires rebalancing of the tree.

Balance factor = Height (left sub-tree) – Height (right sub-tree)

• ·   If the balance factor of a node is 1, then it means that the left sub-tree of the tree is one level higher than that of the right sub-tree. Such a tree is therefore called as a left-heavy tree.
• ·  If the balance factor of a node is 0, then it means that the height of the left sub-tree (longest path in the left sub-tree) is equal to the height of the right sub-tree.(balanced AVL tree.
  )
• ·   If the balance factor of a node is –1, then it means that the left sub-tree of the tree is one level lower than that of the right sub-tree. Such a tree is therefore called as a right-heavy tree.

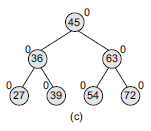
Look at Fig a Left-heavy AVL tree.  Note that the nodes 18, 39, 54, and 72 have no children, so their balance factor = 0. Node 27 has one left child and zero right child. So, the height of left sub-tree = 1, whereas the height of right sub-tree = 0. Thus, its balance factor = 1. Look at node 36, it has a left sub-tree with height = 2, whereas the height of right sub-tree = 1. Thus, its balance factor = 2 – 1 = 1. Similarly, the balance factor of node 45 = 3 – 2 =1; and node 63 has a balance factor of 0 (1 – 1).

Look at Fig b right-heavy AVL tree.  Note that the nodes 70,54,39, and 27 have no children, so their balance factor = 0. Node 72 has one left child and zero right child. So, the height of left sub-tree = 1, whereas the height of right sub-tree = 0. Thus, its balance factor = 1.

 Look at node 63 it has a left sub-tree with height = 1, whereas the height of right sub-tree = 2. Thus, its balance factor = 1 – 2 = -1. Similarly, the balance factor of node 45 = 2 – 3 = -1; and node 36 has a balance factor of 0 (1 – 1).

Look at Fig C. balanced AVL tree.

AVL Rotations

We perform rotation in AVL tree only in case if Balance Factor is other than -1, 0, and 1. There are basically four types of rotations which are as follows:

The Four "out-of-balance" Cases

When the balance factor of just one node is less than -1, or more than 1, the tree is regarded as out of balance, and a rotation is needed to restore balance.

There are four different ways an AVL Tree can be out of balance, and each of these cases require a different rotation operation.

Case	Description	Rotation to Restore Balance
Left-Left (LL)	The unbalanced node and its left child node are both left-heavy.	A single right rotation.
Right-Right (RR)	The unbalanced node and its right child node are both right-heavy.	A single left rotation.
Left-Right (LR)	The unbalanced node is left heavy, and its left child node is right heavy.	First do a left rotation on the left child node, then do a right rotation on the unbalanced node.
Right-Left (RL)	The unbalanced node is right heavy, and its right child node is left heavy.	First do a right rotation on the right child node, then do a left rotation on the unbalanced node.

The first two rotations LL and RR are single rotations and the next two rotations LR and RL are double rotations. For a tree to be unbalanced, minimum height must be at least 2, Let us understand each rotation

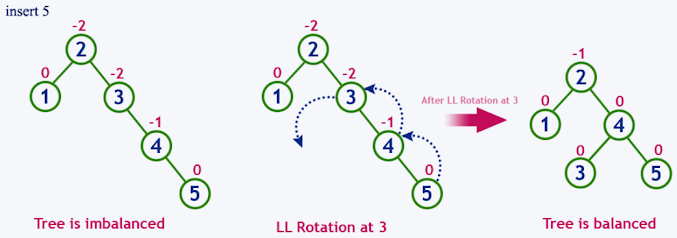
1. LL Rotation

When a node is added into the right subtree of the right subtree, if the tree gets out of balance, we do a single left rotation.

In above example, node A has balance factor -2 because a node C is inserted in the right subtree of A right subtree. We perform the LL rotation on the edge below A.

2. RR Rotation

If a node is added to the left subtree of the left subtree, the AVL tree may get out of balance, we do a single right rotation

In above example, node C has balance factor 2 because a node A is inserted in the left subtree of C left subtree. We perform the RR rotation on the edge below A.

Left-Right Rotation:

A left-right rotation is a combination in which first left rotation takes place after that right rotation executes.

1. Node B has been inserted into the right subtree of A the left subtree of C, because of which C has become an unbalanced node having balance factor 2. This case is L R rotation where: Inserted node is in the right subtree of left subtree of C
2. As LR rotation = LL+RR rotation, hence LL on subtree rooted at A is performed first. By doing LL rotation, node A, has become the left subtree of B.
3. After performing LL rotation, node C is still unbalanced, i.e., having balance factor 2, as inserted node A is in the left of left of C
4. Now we perform RR rotation on full tree, i.e. on node C. node C has now become the right subtree of node B, A is left subtree of B. 
5. Balance factor of each node is now either -1, 0, or 1, i.e. BST is balanced now.

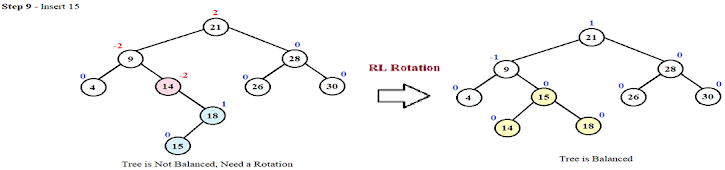
Right-Left Rotation:

A right-left rotation is a combination in which first right rotation takes place after that left rotation executes.

1. Node B has been inserted into the left subtree of C the right subtree of A, because of which A has become an unbalanced node having balance factor - 2. This case is RL rotation where: Inserted node is in the left subtree of right subtree of A
2. As RL rotation = RR rotation + LL rotation, hence, RR on subtree rooted at C is performed first. By doing RR rotation, node C has become the right subtree of B.
3. After performing RR rotation, node A is still unbalanced, i.e. having balance factor -2, which is because of the right-subtree of the right-subtree node A.
4. Now we perform LL rotation on full tree, i.e. on node A. node C has now become the right subtree of node B, and node A has become the left subtree of B.
5. Balance factor of each node is now either -1, 0, or 1, i.e. BST is balanced now.

Advantages of AVL Tree:

AVL trees can self-balance themselves and therefore provides time complexity as O(Log n) for search, insert and delete.

It is a BST only (with balancing), so items can be traversed in sorted order.

Since the balancing rules are strict compared to Red Black Tree, AVL trees in general have relatively less height and hence the search is faster.

AVL tree is relatively less complex to understand and implement compared to Red Black Trees.

Disadvantages of AVL Tree:

It is difficult to implement compared to normal BST and easier compared to Red Black

Less used compared to Red-Black trees.

Due to its rather strict balance, AVL trees provide complicated insertion and removal operations as more rotations are performed.

Applications of AVL Tree:

AVL Tree is used as a first example self balancing BST in teaching DSA as it is easier to understand and implement compared to Red Black

Applications, where insertions and deletions are less common but frequent data lookups along with other operations of BST like sorted traversal, floor, ceil, min and max.

Red Black tree is more commonly implemented in language libraries like map in C++, set in C++, TreeMap in Java and TreeSet in Java.

AVL Trees can be used in a real time environment where predictable and consistent performance is required.

Operations on an AVL Tree

The following operations are performed on AVL tree...

Search

Insertion

Deletion

Search Operation in AVL Tree

In an AVL tree, the search operation is performed with O(log n) time complexity. The search operation in the AVL tree is similar to the search operation in a Binary search tree. We use the following steps to search an element in AVL tree...

 

Step 1 - Read the search element from the user.

Step 2 - Compare the search element with the value of root node in the tree.

Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function

Step 4 - If both are not matched, then check whether search element is smaller or larger than that node value.

Step 5 - If search element is smaller, then continue the search process in left subtree.

Step 6 - If search element is larger, then continue the search process in right subtree.

Step 7 - Repeat the same until we find the exact element or until the search element is compared with the leaf node.

Step 8 - If we reach to the node having the value equal to the search value, then display "Element is found" and terminate the function.

Step 9 - If we reach to the leaf node and if it is also not matched with the search element, then display "Element is not found" and terminate the function.

Insertion Operation in AVL Tree

In an AVL tree, the insertion operation is performed with O(log n) time complexity. In AVL Tree, a new node is always inserted as a leaf node. The insertion operation is performed as follows...

 

Step 1 - Insert the new element into the tree using Binary Search Tree insertion logic.

Step 2 - After insertion, check the Balance Factor of every node.

Step 3 - If the Balance Factor of every node is 0 or 1 or -1 then go for next operation.

Step 4 - If the Balance Factor of any node is other than 0 or 1 or -1 then that tree is said to be imbalanced. In this case, perform suitable Rotation to make it balanced and go for next operation.

Deletion Operation in AVL Tree

The deletion operation in AVL Tree is similar to deletion operation in BST. But after every deletion operation, we need to check with the Balance Factor condition. If the tree is balanced after deletion go for next operation otherwise perform suitable rotation to make the tree Balanced.

Example: Construct an AVL Tree by inserting numbers from 1 to 8.

Step-by-Step Construction of the AVL Tree for the given Sequence 21, 26, 30, 9, 4, 14, 28, 18,15,10, 2, 3, 7

Construct an AVL tree having the following elements:  

H, I, J, B, A, E, C, F, D, G, K, L

1.      Insert H, I, J

 

On inserting the above elements, especially in the case of H, the BST becomes unbalanced as the Balance Factor of H is -2. Since the BST is right-skewed, we will perform LL Rotation on node H.