Combinational Circuits: Unit 3: Part 1

Unit 3: Part 1 

Combinational Circuits

Combinational Circuit Analysis:

     Logic gates can be used to construct combinational circuits. To understand the working principles of a combinational circuit, we should analyze it. Therefore, we should first form a logic function between its inputs and output(s). If needed, we can also form the truth table of combinational circuit based on this representation. The final step in the analysis is representing the combinational circuit by less (or simpler) elements, which is called gate-level minimization.

1.  Logic Function Formation between Input and Output
2.  Boolean Algebra 
3. Gate-Level Minimization
4. Combinational Circuit Implementation:  Truth Table-Based Implementation
5. Combinational Circuit Design

1. Logic Function Formation between Input and Output:

   The first step in analyzing a combinational circuit is forming the logic function between its

inputs and output(s). consider a combinational circuit which gives a relation between input and output by reading the circuit.

Circuit diagram of a combinational circuit

These lead to input/output characteristics of the combinational circuit as follows:

This logic function can be implemented by an HDL in an FPGA. However, some simplifications can be done on it before its implementation.

2.Boolean Algebra

Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or logical Algebra. Boolean algebra was invented by George Boole in 1854.

Rule in Boolean Algebra

Following are the important rules used in Boolean algebra.

• The variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
• Complement of a variable is represented by an overbar (-). Thus, complement of variable B is represented as 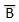. Thus if B = 0 then  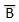= 1 and B = 1 then  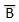= 0.
• ORing of the variables is represented by a plus (+) sign between them. For example ORing of A, B, C is represented as A + B + C.
• Logical ANDing of the two or more variable is represented by writing a dot between them such as A.B.C. Sometimes the dot may be omitted like ABC.

Boolean Laws

There are six types of Boolean Laws.

Commutative law

Any binary operation which satisfies the following expression is referred to as a commutative operation.

Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.

Associative law

This law states that the order in which the logic operations are performed is irrelevant as their effect is the same.

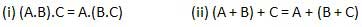
Distributive law

Distributive law states the following condition.

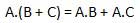
AND law

These laws use the AND operation. Therefore they are called as AND laws.

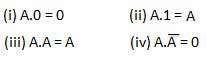
OR law

These laws use the OR operation. Therefore they are called as OR laws.

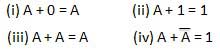
INVERSION law

This law uses the NOT operation. The inversion law states that double inversion of a variable results in the original variable itself.

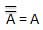
De Morgan's Theorems:

De Morgan has suggested two theorems that are extremely useful in Boolean Algebra. The two theorems are discussed below.

Theorem 1

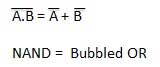The left-hand side (LHS) of this theorem represents a NAND gate with inputs A and B, whereas the right-hand side (RHS) of the theorem represents an OR gate with inverted inputs.

• This OR gate is called a Bubbled OR.

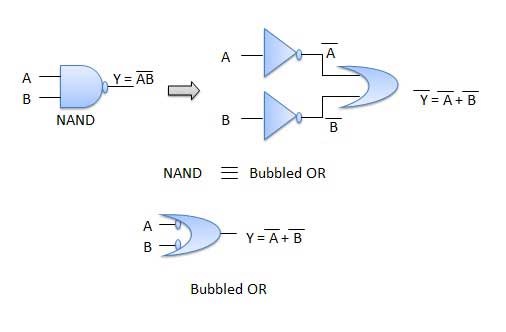
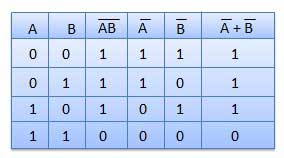
Table showing verification of the De Morgan's first theorem −

Theorem 2

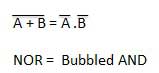The LHS of this theorem represents a NOR gate with inputs A and B, whereas the RHS represents an AND gate with inverted inputs.

• This AND gate is called a Bubbled AND.

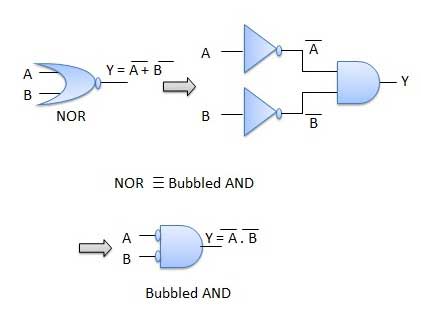
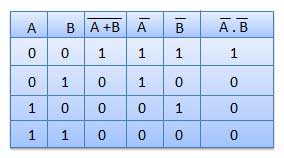
Table showing verification of the De Morgan's second theorem −

Boolean Algebra Identities:

    Let’s assume two binary variables x and y. We can define identities on AND and OR gates

example: Boolean Identity Operations in Verilog

3 Gate-Level Minimization

Gate-level minimization aims to simplify the input/output characteristics of a combinational circuit. The idea here is to obtain the same truth table with less number of logic gates. This operation can be done using Boolean algebra identities and properties.

let’s take the combinational circuit with the logic function z = ~x · y + x ·y. 

    Boolean algebra identity and properties can be used to simplify this logic function such that the end result will be z = y.

In other words, input x does not have any effect on the output of the combinational circuit.

Verilog Description of the Combinational Circuit to be Minimized 

Gate-level minimization example in Vivado

4 Combinational Circuit Implementation: Truth Table-Based Implementation

A combinational circuit can be implemented when its truth table is available. The idea here is focusing on input combinations producing output 0 or 1 separately. Each input combination can be represented by a standard logic function. This leads to the overall logic function of the combinational circuit.

A combinational circuit can be simplified with the help of a truth table we can simplify output function in terms of SOP, POS expression or with help of K-Map.

👉back to main page