Introduction to Red-Black

 Introduction to Red-Black

A Red-Black Tree is a self-balancing binary search tree where each node has an additional attribute: a color, which can be either red or black. The primary objective of these trees is to maintain balance during insertions and deletions, ensuring efficient data retrieval and manipulation.

Red Black Tree is a Binary Search Tree in which every node is colored either RED or BLACK.

Every Red Black Tree has the following properties.

Property #1: Red - Black Tree must be a Binary Search Tree.

Property #2: The ROOT node must be colored BLACK.

Property #3: The children of Red colored node must be colored BLACK. (There should not be two consecutive RED nodes).

Property #4: In all the paths of the tree, there should be same number of BLACK colored nodes.

Property #5: Every new node must be inserted with RED color.

Property #6: Every leaf (e.i. NULL node) must be colored BLACK.

Node Color: Each node is either red or black.

Root Property: The root of the tree is always black.

Red Property: Red nodes cannot have red children (no two consecutive red nodes on any path).

Black Property: Every path from a node to its descendant null nodes (leaves) has the same number of black nodes.

Leaf Property: All leaves (NIL nodes) are black.

Insertion into RED BLACK Tree

In a Red-Black Tree, every new node must be inserted with the color RED. The insertion operation in Red Black Tree is similar to insertion operation in Binary Search Tree. But it is inserted with a color property. After every insertion operation, we need to check all the properties of Red-Black Tree. If all the properties are satisfied then we go to next operation otherwise we perform the following operation to make it Red Black Tree.

 

1. Recolor

2. Rotation

3. Rotation followed by Recolor

The insertion operation in Red Black tree is performed using the following steps...

Step 1 - Check whether tree is Empty.

Step 2 - If tree is Empty then insert the new Node as Root node with color Black and exit from the operation.

Step 3 - If tree is not Empty then insert the new Node as leaf node with color Red.

Step 4 - If the parent of new Node is Black then exit from the operation.

Step 5 - If the parent of new Node is Red then check the color of parent node's sibling of new Node.

Step 6 - If it is colored Black or NULL then make suitable Rotation and Recolor it.

Step 7 - If it is colored Red then perform Recolor. Repeat the same until tree becomes Red Black Tree.

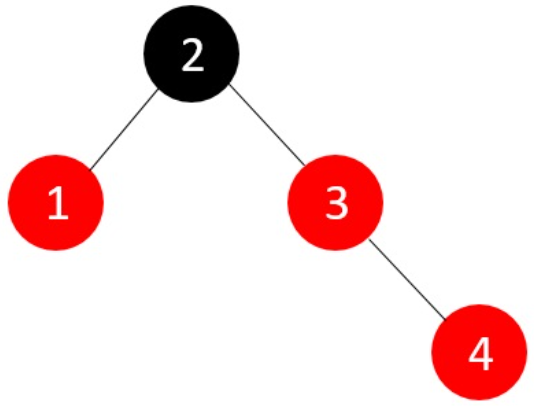
Example:

Create a RED BLACK Tree by inserting the following sequence of numbers 8, 18, 5, 15, 17, 25, 40 & 80.

Sol:

insert (8):  Tree is Empty. So insert newNode as Root node with black color.

insert (18) :  Tree is not Empty. So insert newNode with red color.

insert (5) : Tree is not Empty. So insert newNode with red color.

insert (15) : Tree is not Empty. So insert newNode with red color.

insert (17) : Tree is not Empty. So insert newNode with red color.

insert (25) : Tree is not Empty. So insert newNode with red color.

insert (40) : Tree is not Empty. So insert newNode with red color.

insert (80) : Tree is not Empty. So insert newNode with red color.

finally, the above tree satisfies all the properties of the Red-Black Tree.

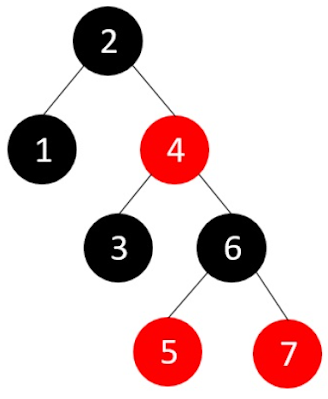
Example 2 :

Let us construct an RB Tree for the first 7 integer numbers to understand the insertion operation in detail

step 1:The tree is checked to be empty so the first node added is a root and is colored black.

Step 2: Now, the tree is not empty so we create a new node and add the next integer with color red,

The nodes do not violate the binary search tree and RB tree properties, hence we move ahead to add another node.

Step 3: The tree is not empty; we create a new red node with the next integer to it. But the parent of the new node is not a black colored node,

 

The tree right now violates both the binary search tree and RB tree properties; since parent's sibling is NULL, we apply a suitable rotation and recolor the nodes.

Step 4:Now that the RB Tree property is restored, we add another node to the tree 

The tree once again violates the RB Tree balance property, so we check for the parent's sibling node color, red in this case, so we just recolor the parent and the sibling.

Step 5:We next insert element 5, which makes the tree violate the RB Tree balance property once again.

And since the sibling is NULL, we apply suitable rotation and recolor.

Step 6: Now, we insert element 6, but the RB Tree property is violated and one of the insertion cases need to be applied 

The parent's sibling is red, so we recolor the parent, parent's sibling and the grandparent nodes since the grandparent is not the root node.

Step 7: Now, we add the last element, 7, but the parent node of this new node is red.

Since the parent's sibling is NULL, we apply suitable rotations (RR rotation)

The final RB Tree is achieved.