Introduction to Red-Black

 Introduction to Red-Black

A Red-Black Tree is a self-balancing binary search tree where each node has an additional attribute: a color, which can be either red or black. The primary objective of these trees is to maintain balance during insertions and deletions, ensuring efficient data retrieval and manipulation.

Red Black Tree is a Binary Search Tree in which every node is colored either RED or BLACK.

Every Red Black Tree has the following properties.

Property #1: Red - Black Tree must be a Binary Search Tree.

Property #2: The ROOT node must be colored BLACK.

Property #3: The children of Red colored node must be colored BLACK. (There should not be two consecutive RED nodes).

Property #4: In all the paths of the tree, there should be same number of BLACK colored nodes.

Property #5: Every new node must be inserted with RED color.

Property #6: Every leaf (e.i. NULL node) must be colored BLACK.

Node Color: Each node is either red or black.

Root Property: The root of the tree is always black.

Red Property: Red nodes cannot have red children (no two consecutive red nodes on any path).

Black Property: Every path from a node to its descendant null nodes (leaves) has the same number of black nodes.

Leaf Property: All leaves (NIL nodes) are black.

Insertion into RED BLACK Tree

In a Red-Black Tree, every new node must be inserted with the color RED. The insertion operation in Red Black Tree is similar to insertion operation in Binary Search Tree. But it is inserted with a color property. After every insertion operation, we need to check all the properties of Red-Black Tree. If all the properties are satisfied then we go to next operation otherwise we perform the following operation to make it Red Black Tree.

 

1. Recolor

2. Rotation

3. Rotation followed by Recolor

The insertion operation in Red Black tree is performed using the following steps...

Step 1 - Check whether tree is Empty.

Step 2 - If tree is Empty then insert the new Node as Root node with color Black and exit from the operation.

Step 3 - If tree is not Empty then insert the new Node as leaf node with color Red.

Step 4 - If the parent of new Node is Black then exit from the operation.

Step 5 - If the parent of new Node is Red then check the color of parent node's sibling of new Node.

Step 6 - If it is colored Black or NULL then make suitable Rotation and Recolor it.

Step 7 - If it is colored Red then perform Recolor. Repeat the same until tree becomes Red Black Tree.

Example:

Create a RED BLACK Tree by inserting the following sequence of numbers 8, 18, 5, 15, 17, 25, 40 & 80.

Sol:

insert (8):  Tree is Empty. So insert newNode as Root node with black color.

insert (18) :  Tree is not Empty. So insert newNode with red color.

insert (5) : Tree is not Empty. So insert newNode with red color.

insert (15) : Tree is not Empty. So insert newNode with red color.

insert (17) : Tree is not Empty. So insert newNode with red color.

insert (25) : Tree is not Empty. So insert newNode with red color.

insert (40) : Tree is not Empty. So insert newNode with red color.

insert (80) : Tree is not Empty. So insert newNode with red color.

finally, the above tree satisfies all the properties of the Red-Black Tree.

B-Tree

 B-Tree

In search trees like binary search tree, AVL Tree, Red-Black tree, etc., every node contains only one value (key) and a maximum of two children. But there is a special type of search tree called B-Tree in which a node contains more than one value (key) and more than two children. B-Tree was developed in the year 1972 by Bayer and McCreight with the name Height Balanced m-way Search Tree. Later it was named as B-Tree.

B trees are extended binary search trees that are specialized in m-way searching, since the order of B trees is 'm'. Order of a tree is defined as the maximum number of children a node can accommodate. Therefore, the height of a b tree is relatively smaller than the height of AVL tree and RB tree. 

They are general form of a Binary Search Tree as it holds more than one key and two children.

 

The various properties of B trees include −

B-Tree of Order m has the following properties...

Property #1 - All leaf nodes must be at same level.

Property #2 - All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.

Property #3 - All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.

Property #4 - If the root node is a non leaf node, then it must have atleast 2 children.

Property #5 - A non leaf node with n-1 keys must have n number of children.

Property #6 - All the key values in a node must be in Ascending Order.

For example:

B-Tree of Order 4 contains a maximum of 3 key values in a node and maximum of 4 children for a node.

order (m)=4

max key (m-1)= 3

Min Key( [m/2] - 1) =1

max Children =4

Min children (m/2) = 2

Construct a B-Tree of Order 3 by inserting numbers from 1 to 10.

order (m)=3

max key (m-1)= 2

Min Key( [m/2] - 1) =1

max Children =3

Min children (m/2) = 2

Insert 1:

Insert 2:

Element '2'is added to existing leaf node. Here, we have only one node and that node acts as root and also leaf. This leaf node has an empty position. So, new element (2) can be inserted at that empty position.

Insert 3:

 Element '3'is added to existing leaf node. Here, we have only one node and that node acts as root and also leaf. This leaf node doesn't has an empty position. So, we split that node by sending middle value (2) to its parent node. But here, this node doesn't has parent. So, this middle value becomes a new root node for the tree.

insert 4:

Element '4'is larger than root node '2' and it is not a leaf node. So, we move to the right of 2: We reach to a leaf node with value '3' and it has an empty position. So, new element (4) can be inserted at that empty position.

Insert 5:

Element '5 is larger than root node '2' and it is not a leaf node. So, we move to the right of'2. We reach to a leaf node and it is already full. So, we split that node by sending middle value (4) to its parent node (2). There is an empty position in its parent node. So, value '4'is added to node with value'2' and new element '5' added as new leaf node.

Insert 6:

Element '6'is larger than root node'2'&'4' and it is not a leaf node. So, we move to the right of '4. We reach to a leaf node with value '5' and it has an empty position. So, new element (6) can be inserted at that empty position.

Insert 7:

Element '7'is larger than root node'2'&'4' and it is not a leaf node. So, we move to the right of '4. We reach to a leaf node and it is already full. So, we split that node by sending middle value (6) to its parent node (2&4). But the parent (284) is also full. So, again we split the node (284) by sending middle value '4' to its parent but this node doesn't have parent, so element 4 become the new root node of tree.

Insert 8:

Element '8'is larger than root node '4' and it is not a leaf node. So, we move to the right of '4. We reach to a node with value '6' '8' is larger than '6' and it is also not a leaf node. So, we move to the right of '6. We reach to a leaf node (7) and it has an empty position. So, new element (8) can be inserted at that empty position.

Insert 9:

Element '9'is larger than root node '4' and it is not a leaf node. So, we move to the right of '4. We reach to a node with value '6, 9 is larger than '6' and it is also not a leaf node. So, we move to the right of '6: We reach to a leaf node (7 & 8). This leaf node is already full. So, we split this node by sending middle value (8) to its parent node. The parent node (6) has an empty position. So, '8'is added at that position. And new element is added as a new leaf node.

Insert 10 :

Element '10' is larger than root node '4' and it is not a leaf node. So, we move to the right of'4. We reach to a node with values '6 & 8.'10' is larger than '6 & 8' and it is also not a leaf node. So, we move to the right of'8'. We reach to a leaf node (9). This leaf node has an empty position. So, new element '10' is added at that empty position.

Construct a B-Tree of Order 5 by inserting numbers from 1 to 20.

order (m)=5

max key (m-1)= 4

Min Key( [m/2] - 1) =2

max Children =5

Min children (m/2) = 3

step 1: 

take root node with 4 keys and start inserting 1,2,3,4

step 2 : now we try insert 5 ,we have already 4 keys in this node so we cannot insert 5 so what we have to do now is here supposed to split this node. 5/2=3(2.5).now key 3 will become root node.

step 3:

similarly 6,7 will be inserted at leaf node. when 8 being inserted, we have already 4 keys in this node so we cannot insert 8 so what we have to do now is here supposed to split this node.

after spliting key 6 will be root node.

step 4:

similarly 9,10 will be inserted at leaf node. when 11 being inserted, we have already 4 keys in this node so we cannot insert 8 so what we have to do now is here supposed to split this node.

after spliting key 9 will be root node.

step 5:

similarly 12,13 will be inserted at leaf node. when 13 being inserted, we have already 4 keys in this node so we cannot insert 13 so what we have to split this node.

after spliting key 12 will be root node.

step 6:

similarly 15,16 will be inserted at leaf node.when 17 being inserted we have already 4 keys in this node so we cannot insert 17 so what we have to split this node.

so node key 15 has to move up to Root node,but root node is also filled ,so splitting in the root node will take place (so that key 9  will go one level up.)

(so that key 9  will go one level up.)

again finally 20 being inserted at leaf node.

key 18 has shifted to up, and splitting done on leaf node.

Construct a B-Tree of Order 5 with following set of  data : D,H,Z,K,B,P,Q,E,A,S,W,T,C,L,N,Y,M

D

H

Z

K

B

P

Q

E

A

S

W

T

C

L

N

Y

M

USE ORDER OF ALPHABETS:

A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.

order (m)=5

max key (m-1)= 4

Min Key( [m/2] - 1) =2

max Children =5

Min children (m/2) = 3

STEP 1: FOLLOW ALPHABETICAL ORDER

INSERT FIRST 4 ELEMENTS

B

P

Q

E

A

S

W

T

C

L

N

Y

M

STEP 2: next insert Key B

STEP 3:next insert Key P

P

Q

E

A

S

W

T

C

L

N

Y

M

STEP 4:next insert Key Q

Q

E

A

S

W

T

C

L

N

Y

M

STEP 5:next insert Key E,A

E

A

S

W

T

C

L

N

Y

M

A

S

W

T

C

L

N

Y

M

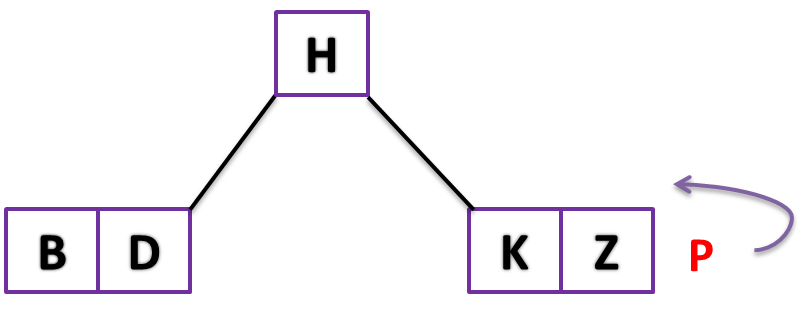
STEP 6: next insert Key S

S

W

T

C

L

N

Y

M

STEP 7: next insert Key W

W

T

C

L

N

Y

M

STEP 8:next insert Key T

T

C

L

N

Y

M

STEP 9:next insert Key C

C

L

N

Y

M

STEP 10:next insert Key L

L

N

Y

M

STEP 11:next insert Key N

N

Y

M

STEP 12:next insert Key Y

Y

M

STEP 13: next insert last Key M

M