QUEUE
Queue is linear data structure and collection of elements. A queue is another special kind of list, where items are inserted at one end called the rear and deleted at the other end called the front.
- The principle of queue is a “FIFO” or “First-in-first-out”.
- Queue is an abstract data structure.
- A queue is a useful data structure in programming.
- It is similar to the ticket queue outside a cinema hall, where the first person entering the queue is the first person who gets the ticket.
Operations on QUEUE:
A queue is an object or more specifically an abstract data structure (ADT) that allows the following operations:
• Enqueue or insertion: which inserts an element at the end of the queue.
• Dequeue or deletion: which deletes an element at the start of the queue.
Representation of Queue (or) Implementation of Queue:
The queue can be represented in two ways:
1. Queue using Array 2. Queue using Linked List
Applications of Queue
Due to the fact that queue performs actions on first in first out basis which is quite fair for the ordering of actions. There are various applications of queues discussed as below.
- Queues are widely used as waiting lists for a single shared resource like printer, disk, CPU.
- Queues are used in asynchronous transfer of data (where data is not being transferred at the same rate between two processes) for eg. pipes, file IO, sockets.
- Queues are used as buffers in most of the applications like MP3 media player, CD player, etc.
- Queue are used to maintain the play list in media players in order to add and remove the songs from the play-list.
- Queues are used in operating systems for handling interrupts.
Array representation of Queue:
We can easily represent queue by using linear arrays. There are two variables i.e. front and rear, that are implemented in the case of every queue.
Front and rear variables point to the position from where insertions and deletions are performed in a queue. Initially, the value of front and rear is -1 which represents an empty queue.
In Fig. above, FRONT = 0 and REAR = 5. Suppose we want to add another element with value 45, then REAR would be incremented by 1 and the value would be stored at the position pointed by REAR.
The queue after addition would be as shown in Fig. above Here, FRONT = 0 and REAR = 6. Every time a new element has to be added, we repeat the same procedure.
If we want to delete an element from the queue, then the value of FRONT will be incremented. Deletions are done from only this end of the queue.
An overflow will occur when we try to insert an element into a queue that is already full. When REAR = MAX – 1, where MAX is the size of the queue, we have an overflow condition.
An underflow condition occurs when we try to delete an element from a queue that is already empty. If FRONT = –1 and REAR = –1, it means there is no element in the queue.
Algorithm to insert an element in a queue
- In Step 1, we first check for the overflow condition.
- In Step 2, we check if the queue is empty. In case the queue is empty, then both FRONT and REAR are set to zero, so that the new value can be stored at the 0th location.
- Otherwise, if the queue already has some values, then REAR is incremented so that it points to the next location in the array.
- In Step 3, the value is stored in the queue at the location pointed by REAR.
Algorithm to delete an element from a queue:
In Step 1, we check for underflow condition. An underflow occurs if FRONT = –1 or FRONT > REAR. However, if queue has some values, then FRONT is incremented so that it now points to the next value in the queue
The process of inserting an element in the queue is called enqueue, and the process of deleting an element from the queue is called dequeue.
#include <stdio.h>
#include <conio.h>
int queue[MAX];
int front = -1, rear = -1;
void insert(void);
int delete_element(void);
int peek(void);
void display(void);
int main()
{int option, val;do{printf(“\n\n ***** MAIN MENU *****”);printf(“\n 1. Insert an element”);printf(“\n 2. Delete an element”);printf(“\n 3. Peek”);printf(“\n 4. Display the queue”);printf(“\n 5. EXIT”);printf(“\n Enter your option : “);scanf(“%d”, &option);switch(option){case 1:insert();break;case 2:val = delete_element();if (val != -1)printf(“\n The number deleted is : %d”, val);break;case 3:val = peek();if (val != -1)printf(“\n The first value in queue is : %d”, val);break;case 4:display();break;}}
while(option != 5);getch();return 0;}
void insert()
{
int num;printf(“\n Enter the number to be inserted in the queue : “);scanf(“%d”, &num);if(rear == MAX-1)printf(“\n OVERFLOW”);else if(front == -1 && rear == -1)front = rear = 0;elserear++;queue[rear] = num;}
int delete_element()
{int val;if(front == -1 || front>rear)
{
printf(“\n UNDERFLOW”);return -1;}else{val = queue[front];front++;if(front > rear)front = rear = -1;return val;}}
int peek()
{if(front==-1 || front>rear){printf(“\n QUEUE IS EMPTY”);return -1;}else{return queue[front];}}
void display()
{int i;printf(“\n”);if(front == -1 || front > rear)printf(“\n QUEUE IS EMPTY”);else{for(i = front;i <= rear;i++)printf(“\t %d”, queue[i]);}
}
Drawback of array implementation:
Memory wastage : The space of the array, which is used to store queue elements, can never be reused to store the elements of that queue because the elements can only be inserted at front end and the value of front might be so high so that, all the space before that, can never be filled.
In above figure shows how the memory space is wasted in the array representation of queue. In the above figure, a queue of size 10 having 3 elements, is shown. The value of the front variable is 5, therefore, we can not reinsert the values in the place of already deleted element before the position of front. That much space of the array is wasted and can not be used in the future (for this queue).
Deciding the array size:
most common problem with array implementation is the size of the array which requires to be declared in advance.
LINKED REPRESENTATION OF QUEUEs:
In case the queue is a very small one or its maximum size is known in advance, then the array implementation of the queue gives an efficient implementation. But if the array size cannot be determined in advance, the other alternative, i.e., the linked representation is used.
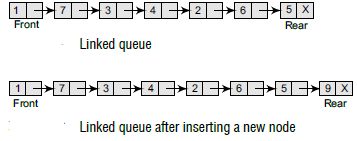
In a linked queue, every element has two parts, one that stores the data and another that stores the address of the next element.
The START pointer of the linked list is used as FRONT. Here, we will also use another pointer called REAR, which will store the address of the last element in the queue.
All insertions will be done at the rear end and all the deletions will be done at the front end. If FRONT = REAR = NULL, then it indicates that the queue is empty.
Operations on Linked Queues:
A queue has two basic operations: insert and delete.
Insert operation
The insert operation is used to insert an element into a queue. The new element is added as the last element of the queue.
To insert an element with value 9, we first check if FRONT=NULL. If the condition holds, then the queue is empty. So, we allocate memory for a new node, store the value in its data part and NULL in its next part. The new node will then be called both FRONT and rear.
However, if FRONT != NULL, then we will insert the new node at the rear end of the linked queue and name this new node as rear.
In Step 1, the memory is allocated for the new node. In Step 2, the DATA part of the new node is initialized with the value to be stored in the node.
In Step 3, we check if the new node is the first node of the linked queue. This is done by checking if FRONT = NULL. If this is the case, then the new node is tagged as FRONT as well as REAR. Also NULL is stored in the NEXT part of the node (which is also the FRONT and the REAR node). However, if the new node is not the first node in the list, then it is added at the REAR end of the linked queue (or the last node of the queue).
struct queue *insert(struct queue *q,int val)
{
struct node *ptr;ptr = (struct node*)malloc(sizeof(struct node));ptr -> data = val;if(q -> front == NULL)
{q -> front = ptr;q -> rear = ptr;q -> front -> next = q -> rear -> next = NULL;}
else
{q -> rear -> next = ptr;q -> rear = ptr;q -> rear -> next = NULL;}
return q;
}
Delete Operation:
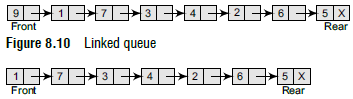
The delete operation is used to delete the element that is first inserted in a queue, i.e., the element whose address is stored in FRONT.
To delete an element, we first check if FRONT=NULL. If the condition is false, then we delete the first node pointed by FRONT. The FRONT will now point to the second element of the linked queue.
In Step 1, we first check for the underflow condition. If the condition is true, then an appropriate message is displayed, otherwise in Step 2, we use a pointer PTR that points to FRONT.
In Step 3, FRONT is made to point to the next node in sequence.
In Step 4, the memory occupied by PTR is given back to the free pool.
struct queue *delete_element(struct queue *q)
{
struct node *ptr;
ptr = q -> front;
if(q -> front == NULL)
printf("\n UNDERFLOW");
else
{
q -> front = q -> front -> next;
printf("\n The value being deleted is : %d", ptr -> data);
free(ptr);
}
return q;
}
Types of Queue
There are four different types of queue that are listed as follows
1. Circular Queue 2. Deque 3. Priority Queue 4. Multiple Queue
Circular Queues:
In linear queues, insertions can be done only at one end called the REAR and deletions are always done from the other end called the FRONT.
Consider a scenario in which two successive deletions are made. The queue will then be given as shown
Suppose we want to insert a new element in the queue shown in above Fig. Even though there is space available, the overflow condition still exists because the condition rear = MAX – 1 still holds true. This is a major drawback of a linear queue.
To resolve this problem,In the circular queue, the first index comes right after the last index.
The circular queue will be full only when front = 0 and rear = Max – 1. A circular queue is implemented in the same manner as a linear queue is implemented. The only difference will be in the code that performs insertion and deletion operations.
For insertion, we now have to check for the following three conditions:
If front = 0 and rear = MAX – 1, then the circular queue is full. Look at the queue given in Fig below
If rear != MAX – 1, then rear will be incremented and the value will be inserted as illustrated in Fig below.
If front != 0 and rear = MAX – 1, then it means that the queue is not full. So, set rear = 0
and insert the new element there, as shown in Fig below.
the algorithm to insert an element in a circular queue.
- In Step 1, we check for the overflow condition.
- In Step 2, we make two checks. First to see if the queue is empty, and second to see if the REAR end has already reached the maximum capacity while there are certain free locations before the FRONT end.
- In Step 3, the value is stored in the queue at the location pointed by REAR.
FOR DELETION:
If front = –1, then there are no elements in the queue. So, an underflow condition will be reported.
If the queue is not empty and front = rear, then after deleting the element at the front the queue becomes empty and so front and rear are set to –1.
If the queue is not empty and front = MAX–1, then after deleting the element at the front,
front is set to 0.
algorithm to delete an element from a circular queue
- In Step 1, we check for the underflow condition.
- In Step 2, the value of the queue at the location pointed by FRONT is stored in VAL.
- In Step 3, we make two checks. First to see if the queue has become empty after deletion and second to see if FRONT has reached the maximum capacity of the queue. The value of FRONT is then updated based on the outcome of these checks.
*******************************
2. Deque:Double Ended Queue (pronounced as ‘deck’ or ‘dequeue’) It is also known as a head-tail linked list because elements can be added to or removed from either the front (head) or the back (tail) end.However, no element can be added and deleted from the middle.
Though the insertion and deletion in a deque can be performed on both ends, it does not follow the FIFO rule. The representation of a deque is given as follows -
Types of deque
There are two types of deque
- Input restricted queue
- Output restricted queue
Input restricted Queue
In input restricted queue, insertion operation can be performed at only one end, while deletion can be performed from both ends.
Output restricted Queue
In output restricted queue, deletion operation can be performed at only one end, while insertion can be performed from both ends.
Operations performed on deque
There are the following operations that can be applied on a deque -
- Insertion at front
- Insertion at rear
- Deletion at front
- Deletion at rear
No comments:
Post a Comment