Binary Search Trees (BST):
A binary search tree, also known as an ordered binary tree. In
a binary search tree, all the nodes in the left sub-tree have a value less than
that of the root node. Correspondingly, all the nodes in the right sub-tree
have a value either equal to or greater than the root node. The same rule is
applicable to every sub-tree in the tree.
In the above figure, we can observe that the root node is
40, and all the nodes of the left subtree are smaller than the root node, and
all the nodes of the right subtree are greater than the root node.
Similarly, we can see the left child of root node is greater
than its left child and smaller than its right child. So, it also satisfies the
property of binary search tree. Therefore, we can say that the tree in the
above image is a binary search tree.
In the above tree, the value of
root node is 40, which is greater than its left child 30 but smaller than right
child of 30, i.e., 55. So, the above tree does not satisfy the property of
Binary search tree. Therefore, the above tree is not a binary search tree.
Example
of creating a binary search tree
Example : State whether the binary trees in below Fig. are binary search trees or not.
Example : Now, let's
see the creation of binary search tree using an example.
Suppose the
data elements are - 45, 15, 79, 90, 10, 55, 12, 20, 50
- First, we have to insert 45 into
the tree as the root of the tree.
- Then, read the next element; if it
is smaller than the root node, insert it as the root of the left subtree,
and move to the next element.
- Otherwise, if the element is larger
than the root node, then insert it as the root of the right subtree.
Now, let's
see the process of creating the Binary search tree using the given data
element. The process of creating the BST is shown below
Example : Create a binary search tree using the following data elements: 45, 39, 56, 12, 34, 78, 32, 10, 89, 54, 67, 81
The search function is used to find whether a given value is present in the tree or not. The searching process begins at the root node.
The function first checks if the binary search tree is empty. If it is empty, then the value we are searching for is not present in the tree. So, the search algorithm terminates by displaying an appropriate message.
However, if there are nodes in the tree, then the search function checks to see if the key value of the current node is equal to the value to be searched.
If not, it checks if the value to be searched for is less than the value of the current node, in which case it should be recursively called on the left child node.
In case the
value is greater than the value of the current node, it should be recursively called
on the right child node.
See the illustration below for a better understanding:
Insert
a value in a Binary Search Tree:
A new key is always inserted at the leaf by maintaining the
property of the binary search tree. We start searching for a key from the root
until we hit a leaf node. Once a leaf node is found, the new node is added as a
child of the leaf node. The below steps are followed while we try to insert a
node into a binary search tree:
v
Initilize the current node (say, currNode or node) with root
node
v
Compare the key with the current node.
v
Move left if the key is less than or equal to the current
node value.
v
Move right if the key is greater than current node value.
v
Repeat steps 2 and 3 until you reach a leaf node.
v
Attach the new key as a left or right child based on the
comparison with the leaf node’s value.
Follow the below illustration for a better understanding:
Deleting a Node from a Binary Search
Tree:
Delete function is used to delete the specified
node from a binary search tree. However, we must delete a node from a binary
search tree so that the property of the binary search tree doesn't violate.
There are three situations in which a node can be deleted from a binary search
tree.
Case 1: Deleting a Node that
has No Children
It is the simplest case, in this case, replace the
leaf node with the NULL and simple free the allocated space.
In the following image, we are deleting the node
85, since the node is a leaf node, therefore the node will be replaced with
NULL and allocated space will be freed.
Case 2:
Deleting a Node with One Child
In
this case, the node’s child is set as the child of the node’s parent (i.e replace
the node with its child).
if the node is the left child of its parent, the node’s
child becomes the left child of the node’s parent. Correspondingly, if the node
is the right child of its parent, the node’s child becomes the right child of
the node’s parent.
In the following image, the node
12 is to be deleted. It has only one child. The node will be replaced with its
child node and the replaced node 12 (which is now leaf node) will simply be
deleted.
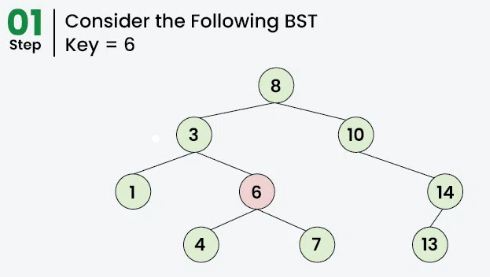
Case 3: Deleting a Node with Two Children
this case, replace the node’s value with its in-order predecessor (largest value in the left sub-tree) or in-order successor (smallest value in the right sub-tree).
Deleting
node 56 from the given binary search tree by replacing node 56 with its
This deletion could also be handled by replacing node 56
with its in-order successor
ex: In the following image, the node 50 is to be deleted which is the root node of the tree.
The in-order traversal of the tree given below 6, 25, 30, 50, 52, 60, 70, 75.
replace
50 with its in-order successor 52. Now, 50 will be moved to the leaf of the
tree, which will simply be deleted.
Delete (TREE, ITEM)
o Step 1:
IF TREE = NULL
Write "item not found in the tree" ELSE IF ITEM < TREE -> DATA
Delete(TREE->LEFT, ITEM)
ELSE IF ITEM > TREE -> DATA
Delete(TREE -> RIGHT, ITEM)
ELSE IF TREE -> LEFT AND TREE -> RIGHT
SET TEMP = findLargestNode(TREE -> LEFT)
SET TREE -> DATA = TEMP -> DATA
Delete(TREE -> LEFT, TEMP -> DATA)
ELSE
SET TEMP = TREE
IF TREE -> LEFT = NULL AND TREE -> RIGHT = NULL
SET TREE = NULL
ELSE IF TREE -> LEFT != NULL
SET TREE = TREE -> LEFT
ELSE
SET TREE = TREE -> RIGHT
[END OF IF]
FREE TEMP
[END OF IF]
o Step 2:
END